Physics around us Lecture 1:From Zeno's "Achill and the Tortoise" paradoxes to Newtonian mechanics and classical physics!
Zeno's paradoxes(芝诺悖论)
Zeno's arguments are perhaps the first examples of a method of proof called reductio ad absurdum also known as proof by contradiction
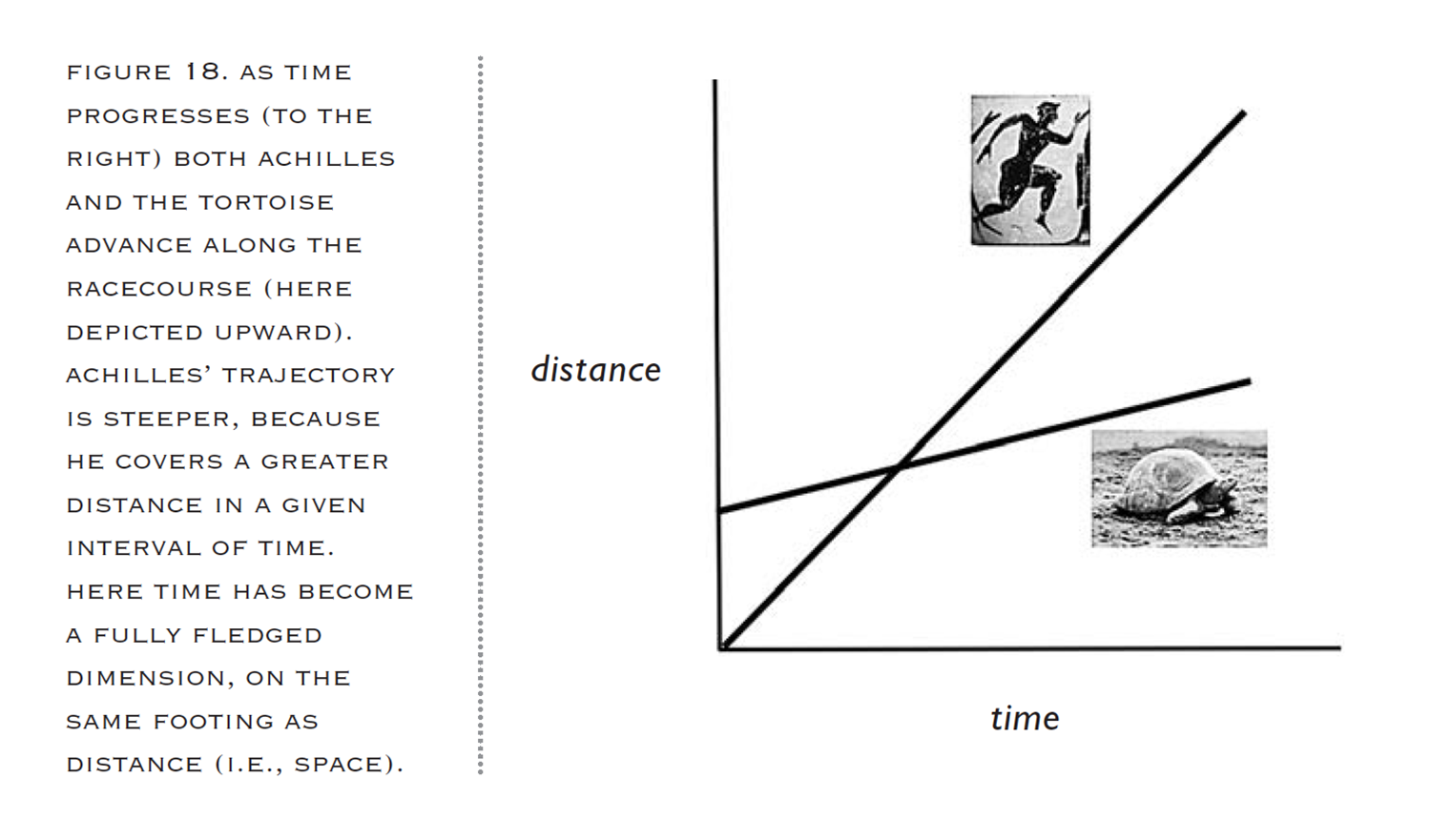
芝诺的论证也许是荒谬归谬法(又称矛盾证明)的第一个例子 ## Achilles and the Tortoise(阿喀琉斯与乌龟) In a race, the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead. – as recounted by Aristotle.
In the paradox of Achilles and the Tortoise, Achilles is in a footrace with the tortoise. Achilles allows the tortoise a head start of 100 meters, for example. If we suppose that each racer starts running at some constant speed (one very fast and one very slow), then after some finite time, Achilles will have run 100 meters, bringing him to the tortoise's starting point. During this time, the tortoise has run a much shorter distance, say, 10 meters. It will then take Achilles some further time to run that distance, by which time the tortoise will have advanced farther; and then more time still to reach this third point, while the tortoise moves ahead. Thus, whenever Achilles reaches somewhere the tortoise has been, he still has farther to go. Therefore, because there are an infinite number of points Achilles must reach where the tortoise has already been, he can never overtake the tortoise.
The Achilles and the tortoise paradox was resolved 2000 years later after the introduction of the notion of the limit and through the summation of an infinite series by employing the mathematical techniques developed by Cauchy, Weierstrass, Dedekind and Cantor.
2000 年后,随着极限概念的引入,以及利用柯西、魏尔斯特拉斯、戴德金和康托尔开发的数学技术对无穷级数求和,阿基里斯与乌龟悖论得以解决。
Dichotomy paradox(二分法悖论)
That which is in locomotion must arrive at the half-way stage before it arrives at the goal– as recounted by Aristotle.
Suppose Homer wants to catch a stationary bus. Before he can get there, he must get halfway there. Before he can get halfway there, he must get a quarter of the way there. Before traveling a quarter, he must travel one-eighth; before an eighth, one-sixteenth; and so on.
This description requires one to complete an infinite number of tasks, which Zeno maintains is an impossibility.
This sequence also presents a second problem in that it contains no first distance to run, for any possible (finite) first distance could be divided in half, and hence would not be first after all. Hence, the trip cannot even begin. The paradoxical conclusion then would be that travel over any finite distance can neither be completed nor begun, and so all motion must be an illusion.
正如亚里士多德所言,运动中的事物必须先到达半程,才能到达目的地。
假设荷马想赶上一辆固定的公共汽车。在到达目的地之前,他必须先走到半路。在走到一半之前,他必须走四分之一的路程。在走完四分之一的路程之前,他必须走完八分之一的路程;在走完八分之一的路程之前,他必须走完十六分之一的路程;以此类推。
这种描述要求一个人完成无限多的任务,芝诺认为这是不可能的。
这个序列还提出了第二个问题,即它不包含第一段要跑的距离,因为任何可能的(有限的)第一段距离都可能被分成两半,因此终究不是第一段。因此,旅行根本无法开始。那么,矛盾的结论就是,任何有限距离的旅行既不能完成,也不能开始,因此所有的运动都必须是一种幻觉。
Arrow paradox(飞矢不动)
If everything when it occupies an equal space is at rest, and if that which is in locomotion is always occupying such a space at any moment, the flying arrow is therefore motionless. – as recounted by Aristotle
In the arrow paradox Zeno states that for motion to occur, an object must change the position which it occupies. He gives an example of an arrow in flight. He states that in any one (duration-less) instant of time, the arrow is neither moving to where it is, nor to where it is not. It cannot move to where it is not, because no time elapses for it to move there; it cannot move to where it is, because it is already there. In other words, at every instant of time there is no motion occurring. If everything is motionless at every instant, and time is entirely composed of instants, then motion is impossible.
Whereas the previous paradoxes divide space, this paradox starts by dividing time—and not into segments, but into points.
芝诺在 “飞矢不动悖论 ”中指出,要发生运动,物体必须改变其所处的位置。他举了一个飞行中的箭的例子。他指出,在任何一个(无持续时间)瞬间,箭既没有移动到它所在的位置,也没有移动到它不在的位置。它不可能移动到它不在的地方,因为没有时间让它移动到那里;它也不可能移动到它在的地方,因为它已经在那里了。换句话说,在时间的每一瞬间,都没有运动发生。如果万物在每一瞬间都是静止的,时间完全由瞬间组成,那么运动就是不可能的。
之前的悖论是划分空间,而这个悖论则是从划分时间开始--不是划分成段,而是划分成点。 ## Quantum Zeno effect In recent times, the Zeno effect made an intriguing appearance in a rather unlikely place — a situation involving the time evolution of a quantum system which is subject to ‘observations’ over a period of time.
The quantum Zeno effect (also known as the Turing paradox) is a situation in which an unstable particle, if observed continuously, will never decay. One can "freeze" the evolution of the system by measuring it frequently enough in its known initial state. The meaning of the term has since expanded, leading to a more technical definition in which time evolution can be suppressed not only by measurement: the quantum Zeno effect is the suppression of unitary time evolution caused by quantum decoherence in quantum systems provided by a variety of sources: measurement, interactions with the environment, stochastic fields, and so on.
最近,芝诺效应在一个不太可能出现的地方--一个量子系统在一段时间内接受 “观测 ”的时间演化情况--出现了。
Aristotelian physics(亚里士多德的物理学)
Gravitation / Levitation - objects are affected by the force that moves these objects to their natural place.
引力/悬浮 - 物体受力的影响而移动到其自然位置。
Straight line motion - in response to this force, the body moves in a straight line at a constant speed
直线运动 - 在这种力的作用下,物体以恒定的速度做直线运动。
The dependence of velocity on density - the velocity is inversely proportional to the density of the medium
速度与密度的关系--速度与介质密度成反比。
The impossibility of vacuum - since the speed of motion in a vacuum would be infinitely large.
不可能存在真空--因为真空中的运动速度将无限大。
All-pervading (penetrating) ether - every point of space is filled with matter
无所不在(穿透)的以太--空间的每一点都充满了物质。
The continuum theory - between atoms there would be a vacuum, so matter can not consist of atoms
连续体理论--原子之间是真空,因此物质不可能由原子组成。
Ether(Aether) - objects from the supermoon (beyond the Moon orbit) world are made of a different matter than the terrestrial
以太--超月(月球轨道之外)世界的物体由不同于地面的物质构成。
Invariable and eternal cosmos - the Sun and planets are perfect, unchangeable spheres.
不变和永恒的宇宙--太阳和行星是完美、不变的球体。
Movement along the circle - the planets make a perfect circular motion.
沿圆周运动--行星做完美的圆周运动。 # Ptolemy geocentric theory(托勒密地心说)
In the Almagest, Ptolemy wrote of his mathematical studies regarding the motions of the planets, the sun and the moon. He presented the so-called geocentric theory, which stated that the earth was the center of the solar system, and that the other planets and the sun revolved around it.